导航：

 蒙特卡洛法| 重识SimC| 反向工程| 时间驱动和事件驱动| 表达式解析| 面向对象的模拟器设计| 机器不掷骰子|

机器不掷骰子
一次攻击，有可确定的c%的暴击率。那么同样条件下进行一次攻击，产生的结果可能有两种：c%的概率暴击，或者(1-c%)的概率不暴击。
同样，攻击是否未命中？是否被招架？躲闪？格挡？偏斜？
一次打出去的嗜血是否触发血涌？一次命中的肉搏是否触发杀戮机器？
你会说：我用rand()可以得到一个随机数，我用随机数落在哪个区间就可以确定攻击结果如何。
机器不掷骰子。你从未想象过计算机是如何得到随机数的。
这一部分将告诉你计算机生成随机数的原理，便于你理解模拟的底层工作机制。
如果你有兴趣编写自己的随机数生成器，在这一部分的后面，我们将以灰谷的ASA-128为例，浅谈一些高速随机数生成器常用的优化手法。

计算机获得随机数的方法，总体来说，由之前产生的随机数Rk-n、Rk-n+1、Rk-n+2、……Rk-2、Rk-1，通过某种杂化算法，推导得到新的随机数值Rk，并且表面上看起来尽可能与之前的序列无关。
说着很复杂，我们举个例子。
假如我们现在只需要得到1到7的随机数。
我们选用的杂化算法是“Rk=Rk-1+5”，如果结果超过7呢，就取一下余数。
比如第一个数是1，那么下一个数就是1+5=6；再下一个数就是6+5=11，11超过了7，所以取余得4。
那么由一个初值1可以得到序列1-6-4-2-7-5-3-……
由一个初值2可以得到序列2-7-5-3-1-……
别看这种算法简单，但是它确实有效，如果对其调节良好，它可以产生循环序列非常长的随机数，而且生成速度也比较快，足够提供给普通应用程序使用了。这种算法称为“线性同余法”，也是C库函数提供的rand()所采用的方法。上面例子中提供的初值(1、2)称为“种子值”，C库函数中使用srand()函数设置种子值。
种子值即初始状态。由于计算机系统是一个确定系统，由确定的初态执行确定的操作，一定会跳转到另一个确定的次态，所以得到的随机数序列只是看起来前后无关，其值其实是确定可求的，并非真正“随机”。
我们管这种随机数发生器(Random Number Generator，RNG)叫做伪随机数发生器(Pseudo RNG，PRNG)。你可以相信，在现有的计算机系统上，所有软件随机数发生器，一定都是伪随机数发生器。
在伪随机数发生器中，由相同的种子值，总是可以引出相同的随机数序列。

在SimC中，你可以通过关键字seed来设置随机数发生器的种子值。
Code (c):
seed=11223344

如果声明了deterministic_rng关键字，则SimC会使用固定的种子值31459。
Code (c):
deterministic_rng=1
#它等价于 seed=31459

如果你使用了多个线程，那么每个线程使用的种子值会递增1，以使它们获得不同的随机数序列。例如零号线程会使用31459，一号线程会使用31460，二号线程会使用31461……
固定了种子值，也就固定了RNG发生的随机数序列。如果包括“线程数”在内的各个模拟参数也都固定，你将得到固定的模拟结果。多次重复模拟，结果不会有一丝一毫的变化。
如果你不设置种子值，那么SimC会使用当前的Unix时间戳作为种子值。所以，你在不同时间进行的模拟，使用的种子值一定不一样，产生的随机数序列也将发生变化。最终现象就是，相同的条件，多次模拟，得到的模拟结果会上下浮动。

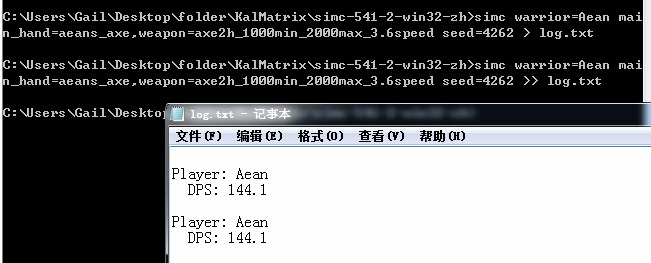
                 图：使用固定的种子值4262进行两次模拟，得到完全相同的结果144.1DPS。

现在工业和学术上的RNG标准，是采用单指令多数据流快速梅森旋转算法(SFMT)，由广岛大学睦齐藤和松本诚所著。
SimC也不例外采用了SFMT。
[http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/SFMT/]
这种RNG产生的随机数质量高，速度快，基于SSE2指令集技术已经成熟，绝大多数现有PC平台都支持SSE2指令集。
随机数可以大量产生，而且迭代间算法相仿，所以非常适合采用单指令多数据流技术进行加速。

可能你会奇怪，老死程总是教导我们，不要轻易重写C库函数，因为它们都做了大量的优化，性能是最好的。
既然C库函数提供了rand()，那么我们为什么还要讨论随机数发生器？为什么还要有SFMT，而且SimC要采用第三方的RNG代替库函数？
那么很遗憾，编写库函数的人并非万能手。rand()在普通的应用中性能是非常出色的，例如你想在屏幕上随机画几条线做屏幕保护程序……
在高速运算中，rand()有三大不足：
精度低
rand()只能生成15比特的随机数，这连一个unsigned short类型都填充不满。要想使用rand()填满一个常用的数据类型，例如32比特的int或者尾码有52比特的double，你必须多次调用rand()将它们的结果拼接在一起。
这种拼接将招来极大的CPU开销，可以让生成速度放慢几倍甚至几十倍。
只能生成整数
rand()生成的是0～32767范围内的随机整数。在模拟中，我们往往都用0～1范围内的浮点数来表达概率。
由整数转型为0~1之间的浮点数的开销，比生成随机数本身的开销还要大。
速度慢
rand()并不会使用任何CPU扩展指令集进行加速。
生成精度低意味着我们需要多次调用它，你还需要蒙受额外的函数调用的开销。
调用库函数会中断编译器对你所写程序的优化。如果你把rand()插得代码里到处都是，你的程序几乎就得不到编译器的照顾了。
下面两张图是rand()和灰谷自己制作的随机数生成器ASA-128的生成速度对比。程序给出了Data Rate(数据填充速率)，它们相差了几十倍。数据可能并不能非常准确地表达它们之间的性能差异，但足够直观。

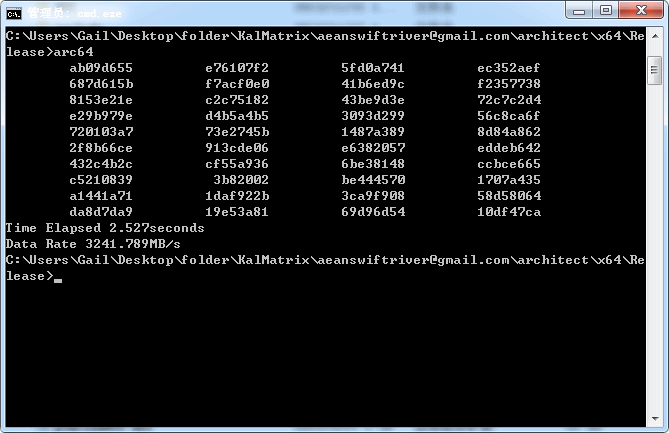
                                                     图：C库函数rand与ASA-128生成速度对比。

SFMT的代码可以在上面给出的链接中找到。
这里我给出ASA-128的代码。要使用它，你应该遵从GNU GPLv3许可。
我简单对其中用到的优化手法进行说明，我们就结束RNG这一部分。
Code (c):
/**
    Aean"s SSE2-Accelerated 128-Bits Pseudo Random Number Generator.
                    Copyright (C) 2013 fhsvengetta
    License:
    This program is free software: you can redistribute it and/or modify
    it under the terms of the GNU General Public License as published by
    the Free Software Foundation, either version 3 of the License, or
    (at your option) any later version. See <http://www.gnu.org/licenses/>.

    Notify:
        This program auto translate random bits into IEEE 754 double type.
    Each double-type random number will use 52-bit of data.
        A SSE2-compatible CPU is required at runtime.
*/

#include <emmintrin.h>
#include <malloc.h>

//=== PRNG Engine ===================================================
                //Force stack-alloc to enhance perf.
#define RNG_STACK_ALLOC
                //If you go on stack overflow, add /STACK:reserve option into link command line
                //, or undef this flag.

#ifndef RNG_STACK_ALLOC
#pragma message("RNG buffer is allocated at heap segment.")
#pragma message("To force stack-alloc for performance, define RNG_STACK_ALLOC in header then rebuild.")
#pragma message("RNG缓冲区被分配在堆上。要强制进行栈分配以提高性能，在头文件定义 RNG_STACK_ALLOC 然后重建。")
#endif

enum {RNG_BUFFER_SIZE = 4096};//Buffer size measured in __m128i (128bits). Must be divisible by 4.
class rng_t{
   private:
      __m128i           r0,r1,r2,r3;
#ifndef RNG_STACK_ALLOC
       unsigned int*   buffer_list;
#else
      unsigned int   buffer_list[RNG_BUFFER_SIZE*sizeof(__m128i)/sizeof(unsigned int)];
#endif
       size_t         buffer_i;
      void generate_buffer(void* bufptr);
   public:
      rng_t() : buffer_i(0){
#ifndef RNG_STACK_ALLOC
         buffer_list = ( unsigned int* )_aligned_malloc( RNG_BUFFER_SIZE * sizeof( __m128i ), 16 );
#endif
      };
#ifndef RNG_STACK_ALLOC
      ~rng_t(){
         _aligned_free(buffer_list);
      };
#endif
      double get(void);
      void set_seed(unsigned int seed);
};

//=== rng_generate_buffer ===========================================
void rng_t::generate_buffer( void* bufptr ) {
    __m128i* p     = ( __m128i* )bufptr;
    register __m128i m;
    register __m128i a0;
    register __m128i a1;
    register __m128i a2;
    register __m128i a3;
    register __m128i m0;
    register __m128i m1;
    register __m128i m2;
    register __m128i m3;
    size_t i = 0;

    //Iterate to fill buffer.
    for( ; i < RNG_BUFFER_SIZE; ) {
//--Loop0--
        //Mask Hybrid.
        m = _mm_set_epi16( 0x200, 0x200, 0x200, 0x200, 0x200, 0x200, 0x200, 0x200 );
        m0 = _mm_set_epi32( 0x1C001C00, 0x1C001C00, 0x1C001C00, 0x1C001C00 );
        m1 = _mm_set_epi32( 0x20002000, 0x20002000, 0x20002000, 0x20002000 );
        m2 = _mm_set_epi32( 0x40004000, 0x40004000, 0x40004000, 0x40004000 );
        m3 = _mm_set_epi32( 0x80008000, 0x80008000, 0x80008000, 0x80008000 );
        a0 = _mm_slli_epi16( r0, 10 );
        a1 = _mm_slli_epi16( r0, 9 );
        a2 = _mm_slli_epi16( r0, 8 );
        a3 = _mm_slli_epi16( r0, 3 );
        a0 = _mm_and_si128( a0, m0 );
        a1 = _mm_and_si128( a1, m1 );
        a2 = _mm_and_si128( a2, m2 );
        a3 = _mm_and_si128( a3, m3 );
        a0 = _mm_or_si128( a0, a1 );
        a2 = _mm_or_si128( a2, a3 );
        a0 = _mm_or_si128( a0, a2 );
        m = _mm_or_si128( m, a0 );
        //Random Number Masking.
        m0 = _mm_add_epi32( r0, r1 );
        m1 = _mm_add_epi32( r2, r3 );
        m0 = _mm_add_epi32( m0, m1 );
        a0 = _mm_srli_epi32( m0, 4 );
        m0 = _mm_xor_si128( m0, a0 );
        a1 = _mm_slli_epi16( m0, 2 );
        a1 = _mm_and_si128( a1, m );
        m0 = _mm_xor_si128( m0, a1 );
        a2 = _mm_slli_epi32( m0, 20 );
        a2 = _mm_and_si128( a2, m );
        m0 = _mm_xor_si128( m0, a2 );
        a3 = _mm_srli_epi32( m0, 18 );
        m0 = _mm_xor_si128( m0, a3 );
        //Store into register & memory.
        r0 = m0;
        _mm_stream_si128( &p[i++], m0 );
//--Loop1--
        //Mask Hybrid.
        m = _mm_set_epi16( 0x200, 0x200, 0x200, 0x200, 0x200, 0x200, 0x200, 0x200 );
        m0 = _mm_set_epi32( 0x1C001C00, 0x1C001C00, 0x1C001C00, 0x1C001C00 );
        m1 = _mm_set_epi32( 0x20002000, 0x20002000, 0x20002000, 0x20002000 );
        m2 = _mm_set_epi32( 0x40004000, 0x40004000, 0x40004000, 0x40004000 );
        m3 = _mm_set_epi32( 0x80008000, 0x80008000, 0x80008000, 0x80008000 );
        a0 = _mm_slli_epi16( r1, 10 );
        a1 = _mm_slli_epi16( r1, 9 );
        a2 = _mm_slli_epi16( r1, 8 );
        a3 = _mm_slli_epi16( r1, 3 );
        a0 = _mm_and_si128( a0, m0 );
        a1 = _mm_and_si128( a1, m1 );
        a2 = _mm_and_si128( a2, m2 );
        a3 = _mm_and_si128( a3, m3 );
        a0 = _mm_or_si128( a0, a1 );
        a2 = _mm_or_si128( a2, a3 );
        a0 = _mm_or_si128( a0, a2 );
        m = _mm_or_si128( m, a0 );
        //Random Number Masking.
        m0 = _mm_add_epi32( r0, r1 );
        m1 = _mm_add_epi32( r2, r3 );
        m0 = _mm_add_epi32( m0, m1 );
        a0 = _mm_srli_epi32( m0, 4 );
        m0 = _mm_xor_si128( m0, a0 );
        a1 = _mm_slli_epi16( m0, 2 );
        a1 = _mm_and_si128( a1, m );
        m0 = _mm_xor_si128( m0, a1 );
        a2 = _mm_slli_epi32( m0, 20 );
        a2 = _mm_and_si128( a2, m );
        m0 = _mm_xor_si128( m0, a2 );
        a3 = _mm_srli_epi32( m0, 18 );
        m0 = _mm_xor_si128( m0, a3 );
        //Store into register & memory.
        r1 = m0;
        _mm_stream_si128( &p[i++], m0 );
//--Loop2--
        //Mask Hybrid.
        m = _mm_set_epi16( 0x200, 0x200, 0x200, 0x200, 0x200, 0x200, 0x200, 0x200 );
        m0 = _mm_set_epi32( 0x1C001C00, 0x1C001C00, 0x1C001C00, 0x1C001C00 );
        m1 = _mm_set_epi32( 0x20002000, 0x20002000, 0x20002000, 0x20002000 );
        m2 = _mm_set_epi32( 0x40004000, 0x40004000, 0x40004000, 0x40004000 );
        m3 = _mm_set_epi32( 0x80008000, 0x80008000, 0x80008000, 0x80008000 );
        a0 = _mm_slli_epi16( r2, 10 );
        a1 = _mm_slli_epi16( r2, 9 );
        a2 = _mm_slli_epi16( r2, 8 );
        a3 = _mm_slli_epi16( r2, 3 );
        a0 = _mm_and_si128( a0, m0 );
        a1 = _mm_and_si128( a1, m1 );
        a2 = _mm_and_si128( a2, m2 );
        a3 = _mm_and_si128( a3, m3 );
        a0 = _mm_or_si128( a0, a1 );
        a2 = _mm_or_si128( a2, a3 );
        a0 = _mm_or_si128( a0, a2 );
        m = _mm_or_si128( m, a0 );
        //Random Number Masking.
        m0 = _mm_add_epi32( r0, r1 );
        m1 = _mm_add_epi32( r2, r3 );
        m0 = _mm_add_epi32( m0, m1 );
        a0 = _mm_srli_epi32( m0, 4 );
        m0 = _mm_xor_si128( m0, a0 );
        a1 = _mm_slli_epi16( m0, 2 );
        a1 = _mm_and_si128( a1, m );
        m0 = _mm_xor_si128( m0, a1 );
        a2 = _mm_slli_epi32( m0, 20 );
        a2 = _mm_and_si128( a2, m );
        m0 = _mm_xor_si128( m0, a2 );
        a3 = _mm_srli_epi32( m0, 18 );
        m0 = _mm_xor_si128( m0, a3 );
        //Store into register & memory.
        r2 = m0;
        _mm_stream_si128( &p[i++], m0 );
//--Loop3--
        //Mask Hybrid.
        m = _mm_set_epi16( 0x200, 0x200, 0x200, 0x200, 0x200, 0x200, 0x200, 0x200 );
        m0 = _mm_set_epi32( 0x1C001C00, 0x1C001C00, 0x1C001C00, 0x1C001C00 );
        m1 = _mm_set_epi32( 0x20002000, 0x20002000, 0x20002000, 0x20002000 );
        m2 = _mm_set_epi32( 0x40004000, 0x40004000, 0x40004000, 0x40004000 );
        m3 = _mm_set_epi32( 0x80008000, 0x80008000, 0x80008000, 0x80008000 );
        a0 = _mm_slli_epi16( r3, 10 );
        a1 = _mm_slli_epi16( r3, 9 );
        a2 = _mm_slli_epi16( r3, 8 );
        a3 = _mm_slli_epi16( r3, 3 );
        a0 = _mm_and_si128( a0, m0 );
        a1 = _mm_and_si128( a1, m1 );
        a2 = _mm_and_si128( a2, m2 );
        a3 = _mm_and_si128( a3, m3 );
        a0 = _mm_or_si128( a0, a1 );
        a2 = _mm_or_si128( a2, a3 );
        a0 = _mm_or_si128( a0, a2 );
        m = _mm_or_si128( m, a0 );
        //Random Number Masking.
        m0 = _mm_add_epi32( r0, r1 );
        m1 = _mm_add_epi32( r2, r3 );
        m0 = _mm_add_epi32( m0, m1 );
        a0 = _mm_srli_epi32( m0, 4 );
        m0 = _mm_xor_si128( m0, a0 );
        a1 = _mm_slli_epi16( m0, 2 );
        a1 = _mm_and_si128( a1, m );
        m0 = _mm_xor_si128( m0, a1 );
        a2 = _mm_slli_epi32( m0, 20 );
        a2 = _mm_and_si128( a2, m );
        m0 = _mm_xor_si128( m0, a2 );
        a3 = _mm_srli_epi32( m0, 18 );
        m0 = _mm_xor_si128( m0, a3 );
        //Store into register & memory.
        r3 = m0;
        _mm_stream_si128( &p[i++], m0 );
    }
}

 

//=== rng_set_seed ==================================================
void rng_t::set_seed( unsigned int seed ) {
    short low = seed & 0xffff;
    short high = seed >> 16;
    r0 = _mm_set_epi16( high, high + 1, high, high + 2, high + 1, high, high + 2, high );
    r1 = _mm_set_epi16( low + 1, low, low + 2, low, low, low + 1, low, low + 2 );
    r2 = _mm_set_epi16( 5797, 4262, 8015, 3571, 12160, 6087, 6086, 7939 );
    r3 = _mm_set_epi16( 2306, 14613, 14614, 14615, 4849, 4850, 4851, 4852 );
}

//=== rng_get =======================================================
double rng_t::get( void ) {
    union                   {
        double as_double;
        unsigned int as_uint[2];
    } bit_to_double;
    if( buffer_i <= 1 ) {
        buffer_i = RNG_BUFFER_SIZE * sizeof( __m128i ) / sizeof( unsigned int ) - 1;
        generate_buffer( buffer_list );
    }
   /**
      All x86 architectures are little-endian.
      If you want to make this code running on big-endian processors,
      you should swap as_uint[1] / as_uint[0].
   */
    bit_to_double.as_uint[1] = ( buffer_list[buffer_i--] & 0x3FFFFFFF ) | 0x3FF00000;
    bit_to_double.as_uint[0] = buffer_list[buffer_i--];
    bit_to_double.as_double -= 1.0l;
    return bit_to_double.as_double;
}

其实代码并不长，SSE2代码的格式可能看起来比较难受，因为其实它已经属于一种内嵌汇编了。

ASA-128只输入序列中前四个随机数作为参数计算得到下一个。所以这里采用循环展开，在一次For循环中直接完成四组随机数，裁去了一个记录循环队列首尾位置的控制量。
关于循环展开，这是一种非常常见的性能优化手法，如果你不明白是什么意思，可以搜索一下相关资料，这里就不再浪费篇幅去讲。

针对CPU的流水线和乱序执行特性，指令在排序时需要尽可能降低上下文相依性(即下一条指令尽量不要用到上一条指令的结果)。
例如要计算s=a+b+c+d+e+f+g+h，正常的算法是：
s=a+b
s=s+c
s=s+d
s=s+e
s=s+f
s=s+g
s=s+h
但是这全部七条指令都前后相依。例如第一条指令中红色的s的值不计算完毕，就无法计算下一条指令的s，因为下一条指令需要红色的s作为一个操作数。
如果改为：
s=a+b
c=c+d
e=e+f
g=g+h
s=s+c
e=e+g
s=s+e
这时前四条指令都完全互相无关，直到第五条指令才用到第一条指令的结果，指令上下文相依性就变得很小，CPU流水线的效率才能得以最大程度地发挥。

由于生成的是随机比特，也就是整数。整数到浮点数的转换是一大开销热点。
普通的转换方法，是通过整数到浮点数的转型，和一次浮点除法完成的。例如：
Code (c):
int r_int = rand(); //r_int是[0, 32768)区间内的整数随机数。
double r_double = static_cast<double>(r_int); //由整数到浮点数的强制转型，现在r_double是[0.0, 32767.0]区间内的浮点随机数。
r_double = r_double / 32768.0l; //通过一次浮动除法，现在r_double是[0.0, 1.0)区间内的浮点随机数。
return r_double

整数到浮点数的转型开销大约在4～16个时钟周期，浮点除法需要20～45个时钟周期。
如果能够避免它们，转换速度将会呈几十倍的速度提升。

按照IEEE 754的双精度浮点数标准，浮点数1.0的二进制表示为：
0011 1111 1111 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
而小于2.0的、双精度所能表示的最大浮点数1.9999999999999997779553950749686919152736663818359375，它的二进制表示为：
0011 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111
我们注意到，[1.0, 2.0)区间内的双精度浮点数，固定由“0011 1111 1111”组成高12位；低52位从全0一直变化到全1。
所以如果我们刻意制造一块内存，在其高12位填充“0011 1111 1111”，然后在其低52位填充随机比特，就可以得到[1.0, 2.0)区间的浮点随机数了。
要得到[0.0, 1.0)区间的浮点随机数，只需做一次浮点减法，让其值自减1.0。浮点减法的开销是非常小的。
Code (c):
union                  {
    double as_double;
    __int64 as_int;
}r; //union                  联合体，同一块内存空间r，既可以解释为64位整数，也可以解释为双精度浮点数。
//这样我们就能对浮点数进行按位逻辑运算，直接操作其中的比特。正常情况下，只有整数才接受按位逻辑运算。
r.as_int = rand(); //假设rand()提供了64比特的随机数据，按照整数存入r中。
//我们现在把它按照IEEE 754的双精度浮点数标准进行格式化。
r.as_int = ( r.as_int & 0x3FFFFFFFFFFFFFFF ) | 0x3FF0000000000000; //通过两次位逻辑运算，将r的高12位(1位符号位，11位阶码)
                                                             //设置为“0011 1111 1111”。后52位尾码维持不变。
                                                             //现在r就是[1.0, 2.0)区间内的浮点随机数了。
r.as_double -= 1.0l; //做一次浮点减法，就得到了[0.0, 1.0)区间内的浮点随机数。
return r.as_double;

这种转换的开销只有一次位与运算，一次位或运算，和一次浮点减法。它们都是开销最小的计算，每条指令都可在1个时钟周期内完成。

小结
这个系统太大了，如果要全部写下来，恐怕要成为一本教科书。
内容庞杂，思路不是很清晰，这次写出来的东西像是一块一块的东西拼凑起来的。篇幅看起来很长，其实不到五万字。
可能遗漏了很多应该提及的内容，但我现在已经不知道再讲些什么好了。讲SimC属性权值是如何评的？拜托这你自己应该弄明白的。
所以先只来这么多。如果有必要，我再看情况往这里添加内容，或者干脆再来一个模拟器组成原理第二篇。

对于有心了解模拟器技术的人，这可能足够他们入门，至少是了解一点模拟器的思想。
更加展开的内容，你可以试试点击主楼的参考文献，它们指向四面八方，包含各式各样的资料。
有些只是引用了一句话；有些则是本应出现在文中却因篇幅问题被挤在外面的科学论文。