侏儒在各种奇幻作品中一直被描写为科技发达的种族。这其中是有原因的。
好，那你来猜猜？那绝对绝对绝对不是主要的因素。
人类、精灵一类的种族都有五根手指，所以他们的数学一定采用的是十进制。
而侏儒只有四根手指。他们在启蒙时期更有可能会采用八进制的计数法，并在此基础上演化出自己的数学。
每一位八进制数可以对应转化为三位二进制数。这一点十进制做不到，所以当今地球上的我们还有在使用BCD码之类的搞笑的东西。
我们的第一台电子计算机是十进制的。第一台机电计算机也都是十进制的。确定采用二进制是冯·诺依曼体系之后的事情。
假如人类也只有四根手指，人类的信息技术革命可能要提前几个世纪就发生。
这个论点是不是本身就很新鲜？很多人可能我不说都不会注意到侏儒只有四根手指。

 
  图：侏儒娘的四根手指。

多用符合世界本源的眼光来看待事物。否则你很难进步。

是时候展现真正的技术了！

我曾经因为SimC有关的问题几次与其他人争执过。并不是因为我有SimC崇拜之类的毛病，而是大多数人对这个东西的认知层面着实太浅。
打嘴炮是没有用的，现在我是来做实务的。我会以SimC为例，来谈谈DPS模拟器的组成原理。
这篇帖子不会告诉你如何使用SimC，但如果这篇帖子所述的内容你不能透彻了解的话，你就绝不能算作会用SimC的人。
SimC不是一个应用软件，它是一个开源的、社区开发的研究工具。这意味着你有很多研究项目需要深入到SimC的C++源码当中去，而不是简单的导入-跑-得结果的傻瓜三步曲。
我会把我所知道的重点尽可能地写出来。由于这个系统非常庞杂，不可能事无巨细全都写出来，但在你读懂这篇内容之后，加上少许编程功底，应该就能够达到自制DPS模拟器的水平。

本篇将重点放在组成原理上。
导航：
 蒙特卡洛法| 重识SimC| 反向工程| 时间驱动和事件驱动| 表达式解析| 面向对象的模拟器设计| 机器不掷骰子|

蒙特卡洛法
你的微积分学得好吗？
如果好的话，我给你出一个求定积分的问题，让你展示展示真正的实力吧！
如果你是985名校的理科学霸你肯定已经开始摩拳擦掌了。
那么看题：
定积分 I = ∫01|logarcsin(0.5x+0.5)(x+2)/(x+1)|-xsinπxdx，求 I 的值？

好吧我知道你看完之后特别想抄起高树课本糊我一熊脸。哪有这么扯淡的定积分啊！
没错，式子是我瞎编的，编的目的也是让它的形式尽可能地扯淡，让你即使微积分考试考到120分也无从下手。
这个定积分的值，牛顿-莱布尼兹已经完全束手无策了，它的值人类有可能求出来吗？
当然是可以的，而且有多种办法。
我不知道数学家对这种形式一个比一个扯淡的积分有什么对策。作为一个死程，我知道，你可以使用机械求积法，或者Romberg法，它们能在计算机上求得任意精度的积分值。

当你了解了Romberg法后，你会发现，除非你致力于数学理论研究，你所学的微积分知识对求解积分一点意义都没有。
而我，微积分考试只能考20来分，却能将任意形式的积分求解到任意精度。
这可真是个讽刺。

是不是觉得Romberg法非常碉堡？那么我们继续。

二重积分 I = ∫01dy∫0y|logarcsin(0.5x+0.5)(x+2)/(x+1)|-xsinπxdx，求 I 的值？

Romberg法可以求解多重积分吗？我不知道，坦诚的讲，数值分析这门课我也只考了54分。

还有办法求解它吗？
抬头看一眼这一部分的标题。这就引入了我们的主题，Monte Carlo 方法。
在DK区跟人打嘴炮的那次经历是我在NGA闹得最凶残的一次了。你知道的为此我还吃了块抹布。
那次我曾经说过，“蒙特卡洛法是人类的希望。”然后他们都笑我。
现在，面对这个扯淡的重积分，这句话可就不太好笑了。我们先枪毙了微积分中的牛顿-莱布尼兹法，然后又枪毙了数值分析中的龙贝格外推法。
不过你记着，再复杂的问题，都无法阻止蒙特卡洛法。
(对于这个二重积分，最笨拙的机械求积法仍然可行。机械求积法好像永远都是可行的，因为它本身其实就是“积分”的定义。)

通常蒙特卡洛法通过构造符合一定规则的随机数来解决数学上的各种问题。
对于那些由于计算过于复杂而难以得到解析解或者根本没有解析解的问题，蒙特卡洛法是一种有效的求出数值解的方法。
简单地说，蒙特卡洛法可以绕过传统确定性方法中必经的解析这一步，而直接由大量重复实验统计得出数值。在解析十分困难甚至根本不可能予以解析的问题上，蒙特卡洛法将是拯救你的希望所在。

上述问题中，那个积分式描绘了一个三维空间里的几何体。而积分值就是几何体的体积。
这很简单。用一个非常容易计算体积的长方体，框住这个待求积分。然后在此长方体内反复进行随机抽样，每次抽取一个位置完全随机的点，判断该抽样点是否落在待求积分之内。
经过大量的抽样实验后，统计抽样点落在积分内的次数，并与总实验次数相比。
其次数之比，会随着抽样实验次数的增加，而逐渐收敛于积分值与所选长方体体积之比。
求得的数值解与真实值之间的差，称为统计误差。统计误差大小与实验次数的二分之一次幂成反比。这是蒙特卡洛法的收敛速度，实验次数扩大四倍，误差就缩小一半。

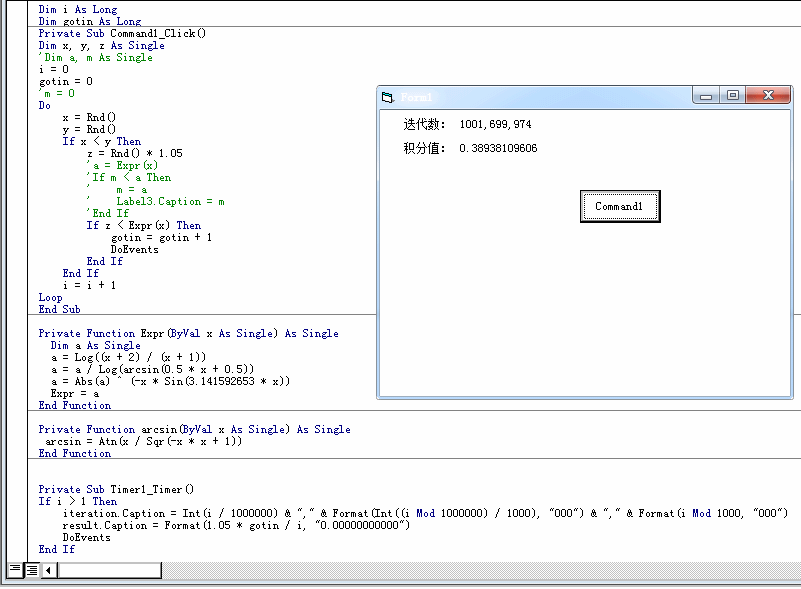
                                                               图：上述二重积分的蒙特卡洛解法程序，及其十亿次抽样模拟解。

这个收敛速度与传统的确定性方法相比，并不快。当实验次数很少的时候，误差会非常大。要想缩减误差，实验次数就需要成倍成倍地增加。
人工进行上万次甚至几亿、几万亿次实验并统计结果是不可能实现的。
这也是为什么蒙特卡洛法在电子计算机发明后才成为一种科学方法，在电子计算机普及后才得以广泛应用。
然而这并不是什么坏事。可以预见的是，随着电子计算机的迅猛发展，进行大量实验的成本越来越低，蒙特卡洛法必将成为推动人类认知进步的重要力量。

你说它的收敛速度是指数级的，太慢；而你不要忘记电子计算机计算能力的发展速度也是指数级的。

蒙特卡洛法，使用大量重复仿真随机实验，得到统计值作为所求问题的数值解。
我们来总结它的优点和缺点。
优点：
无需解析。
在传统的确定性方法中，你永远都逃不掉解析这一步。问题越复杂，解析就越困难。
而对于蒙特卡洛法，无论问题复杂到什么程度，进行随机实验的难度几乎都不受影响。以积分为例：无论积分式多么变态，我只需带入随机点的坐标求值，然后做一次比较大小，然后记录结果；整个过程不需要对式子本身做任何变形。
准确。
在传统的确定性方法中，解析过于困难，所以你有时不得不进行一些近似替代，以简化问题，降低问题的解析难度。
在蒙特卡洛法中，没必要简化。你可以建一个精确的、一点近似都没有的模型，然后研究它。这种模型必然比传统方法的经过近似简化过的模型更接近实际结果。
容易开发。
刨除求积这种简单的数学问题不谈。一个真实环境的模拟程序，在任何带有面向对象特性的计算机程序设计语言上，都可以轻松实现。代码易纠错，易修改，易维护。
想想套用一堆公式制作的WoW解析表格，暴雪只要稍微动一动RPPM触发机制，它们所有与触发有关的内容都需要推翻重做。而模拟器只要跟随着暴雪进行平行改动即可。
精度可控。
蒙特卡洛法所建模型往往准确度更高，系统误差很小。所以要想得到令人信服的结论，只需提高计算精度，缩减统计误差即可。我们可以通过增加运算迭代次数，统计误差可以控制在任意限度之内。
传统解析模型几乎没有统计误差，它们要提高结论的可信程度，就需要缩减系统误差。那可是需要改进自身架构，甚至需要推翻重做才能实现的梦想。
缺点：
计算量大。
受制于蒙特卡洛法的收敛速度，要得到精确的结论，需要大量计算迭代次数的支持。那需要CPU性能和你的时间。
传统解析模型只要建好模，很快就能得到精确结论——虽然不一定准确。(精确意味着统计误差小，准确意味着模型的系统误差小)
只有数值解，没有解析过程。
如果这也算作缺点的话。有时候，面对那些脑筋还沉浸在传统确定性方法中无法自拔的人，你跳过了解析过程，它们就不相信你的结论。
其实我更愿意把它当作优势。
输入量微小变化产生的结果变化，淹没在统计噪音中。
这是真的。指望SimC，你很难模拟“2548命中、15081精通”与“2559命中、15070精通”两种重铸方案孰优孰劣。
除非你很有定力，能独立于山巅，任由风霜侵袭，直至沧海变为桑田，高山沉入海底。玄牛砮皂一定是刚刚拿到一份这样的模拟结果。